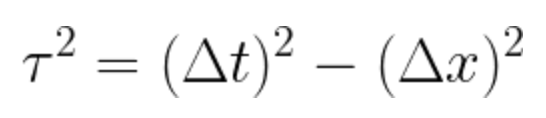
I love the niche this series is targeting:
The Biggest Ideas in the Universe is dedicated to the idea that it is possible to learn about modern physics for real, equations and all, even if you are more amateur than professional and have every intention of staying that way. It is meant for people who have no more mathematical experience than high school algebra, but are willing to look at an equation and think about what it means.
Though I've had more math education than that, I've also forgotten a lot of it, so this sounded like the perfect level of explanation for me.
How successful is this attempt to make physics accessible? Until the last two chapters - on gravity and black holes - I think it does pretty well. I had to reread and think about things a few times, but the effort paid off. I suspect I would have needed to invest significantly more time to really follow the final chapters, but I at least gleaned a little from them. I'm looking forward to the next two volumes.
Cool stuff. My mind was blown a little bit by the explanation of why gravity follows an inverse-square law. It's so simple yet somehow I'd never heard it before: the inverse-square law is a consequence of the fact that in 3-dimensional space, the area of a sphere is proportional to the radius squared.
If we draw a sphere centered on the sun, the lines of force all pass through that sphere. If we draw another sphere with a bigger radius, the same lines will pass through it, but they will be more spread out—fewer lines will pass through any fixed area of the sphere.
I also enjoyed the explanation of why "almost every oscillating system is approximated by a simple harmonic oscillator", which relies on just a little algebra and calculus showing that typically only the squared term in the potential energy function will be significant.
Taxonomy. Carroll explains that physical theories can be categorized as either classical or quantum and also as relativistic or non-relativistic. This book discusses both kinds of classical theories (including Newtonian mechanics and general relativity) but leaves quantum mechanics for a future volume.
He also contrasts local theories with global theories. As I understand it, the difference is whether you make predictions directly based on a single data point, or by using a rule to select from all the predictions that are consistent with a set of data points. Two examples he discusses are Newtonian mechanics and Lagrangian mechanics: they both make identical predictions about the path an object will follow. In the former, you find this path by applying a formula based on the object's state at one point in time. In the latter, you consider all possible paths between the object's states at two points in time and choose the one that minimizes a specific quantity.
Geometry. A few years ago I'd just moved to a new city and was also trying - or at least, aspiring - to beef up my math skills, so I signed up for a local math meetup. I bought the book they were reading at the time, Tensor Analysis on Manifolds, despite not knowing what a tensor or a manifold was or why anyone would need to analyze them. (I never went, and the book has been collecting dust.)
After reading Carroll's chapter on geometry, now I sort of know! A manifold is a way of describing a space, potentially a non-Euclidean space (one that's curved, where parallel lines can intersect or diverge). To fully specify the curvature of a manifold, all you need is a function called a line element that tells you the length of the curve between any two given points. A matrix called a metric tensor is a compact way to express the same information as the line element. This is relevant to physics, of course, because relativity tells us that spacetime is not actually Euclidean, and we need a way to talk about precisely what it is instead.
Relativity. Carroll's discussion of coordinate time vs proper time was illuminating for me:
Now there are two distinct notions of what is meant by "time." One notion of time is as a coordinate on spacetime. Spacetime is a four-dimensional continuum, and if we want to specify locations within it, it's convenient to attach a nunmber called "the time" to every point within it. That's generally what we have in mind when we think of "6 p.m." and "7 p.m." Those refer to values of a coordinate on spacetime, labels that help us locate events. Everyone is supposed to understand what we mean when we say "meet at the restaurant at 7 p.m."
But, says relativity, just as the distance as the crow flies is generally different from the distance you actually travel between two points in space, the duration of time that you experience along your world line generally won't be the same as the universal coordinate time. You experience an amount of time that could be measured by a clock that you carry with you on the journey. This is the proper time along the path. And the duration measured by a clock, just like the distance traveled as measured by the odometer on your car, will depend on the path you take.
And things get weird because:
In space, a straight line describes the shortest distance between two points. In spacetime, by contrast, a straight path yields the longest elapsed time between two events.
So instead of the Pythagorean theorem's sum-of-squares, proper time is calculated using the difference of squares of coordinate time and distance (equation 6.2, page 152):
(The same fact can be expressed in a metric tensor by having "a minus sign for the timelike direction. A metric with this kind of minus sign is called Lorentzian...")
Thus, you experience more time if you sit still from 6pm to 7pm than if you leave on a round-trip journey at 6pm and arrive back where you started at 7pm. Carroll's explanations do a good job of making this weird aspect of reality seem somewhat less mysterious.