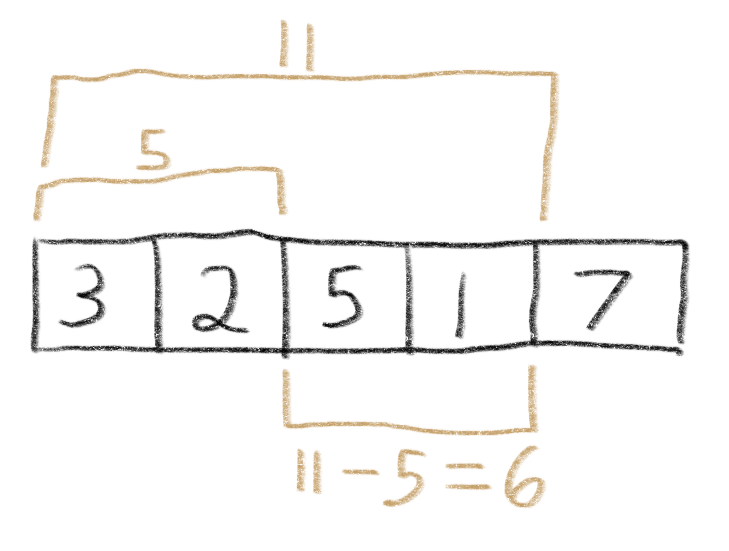
Posted on 2019-06-28
The “Maximum Subarray Sum” problem on HackerRank is challenging, but has an elegant solution. Below, I briefly discuss an inefficient brute force solution, then explain the more efficient approach.
My solutions are written in Kotlin.
I’ll just show how to implement the maximumSum function; for the main function, see the template that HackerRank provides.
If you just want hints, without the full solution, see: June KC Code Challenge Hints.
Table of Contents:
The easiest approach is to simply calculate the modulo-sum of each possible subarray, keeping track of the maximum modulo-sum that we’ve seen as we go along.
To do that, we can use an outer loop that calculates a modulo-sum starting from each index of the array, with an inner loop that adds each subsequent value to it and performs the modulo. At each step of the inner loop, we’ll know the modulo-sum between the index chosen by the outer loop and the index chosen by the inner loop.
fun maximumSum(a: Array<Long>, m: Long): Long { var max = 0L for (i in 0 until a.size) { var sum = 0L for (j in i until a.size) { sum = (sum + a[j]) % m max = maxOf(sum, max) } } return max }
The outer loop runs N times (where N is the length of the array), and each of those iterations runs the inner loop up to N times, so the time complexity of this approach is O(N2).
The problem specifies that the sum of N across all the times this function might be called within a given test input could be as high as 5 * 105, in which case N2 would be 250 billion. You won’t be able to run 250 billion iterations within HackerRank’s time constraints; we need a faster solution.
(On the bright side, the space complexity of this approach is O(1), excluding the input array.)
I was stuck on the problem for a while, so I tried to come up with simpler subproblems that might teach me something useful about it. The one that finally helped me was: given a pair of indices (i, j) specifying a subarray, how can we efficiently find the modulo-sum for that subarray? Assume we’ll be given many pairs of indices, and want something faster than just looping over all elements of the subarray for each pair.
First, consider how we’d approach this if modulo weren’t involved, and we were only concerned with regular sums. The answer will probably have something to do with saving partial sums. So let’s think about how the sums of different subarrays relate to each other.
Consider an array containing [3, 2, 5, 1, 7]:
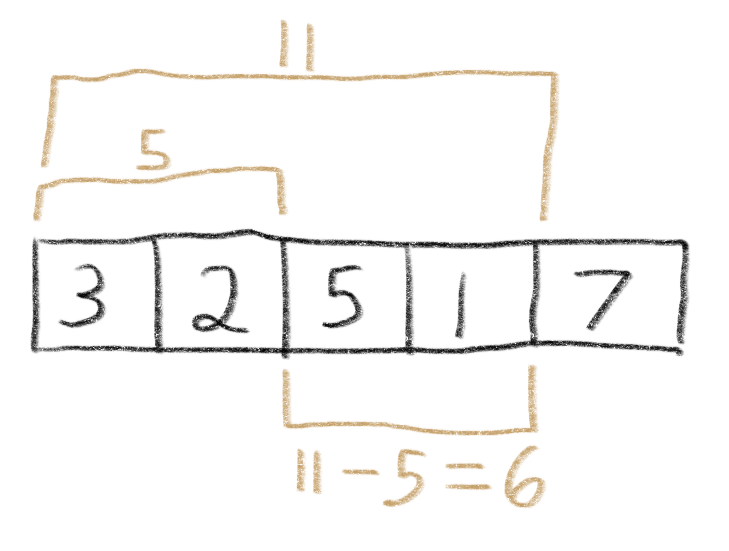
Notice that the sum of subarray 2 to 3 is equal to the sum of subbary 0 to 3, minus the sum of subarray 0 to 1. More generally, for any subarray i to j, the sum equals the sum of subarray 0 to j minus the sum of subarray 0 to i-1.
So, if we precalculate all the sums from index 0 to every other index, we can use them to quickly calculate the sum of any other subarray that we’re asked about. That precalculation can be done with a single pass through the array. All we need is to keep a running total as we go along, and store the total at each step into another array.
Code for that algorithm could look like this:
class SubarraySumFinder(val a: Array<Long>) { val sums = ArrayList<Long>() init { var sum = 0L for (v in a) { sum += v sums.add(sum) } } fun sum(i: Int, j: Int) = sums[j] - (if (i > 0) sums[i - 1] else 0L) } fun main() { val test = SubarraySumFinder(arrayOf(3L, 2L, 5L, 1L, 7L)) println(test.sum(0, 1)) // prints 5 println(test.sum(0, 3)) // prints 11 println(test.sum(2, 3)) // prints 6 println(test.sum(0, 4)) // prints 18 }
The initialization process is O(N) time complexity, and then we can calculate any given subarray’s sum in O(1) time.
What would we have to change from the algorithm in the previous section to find modulo-sums rather than plain sums?
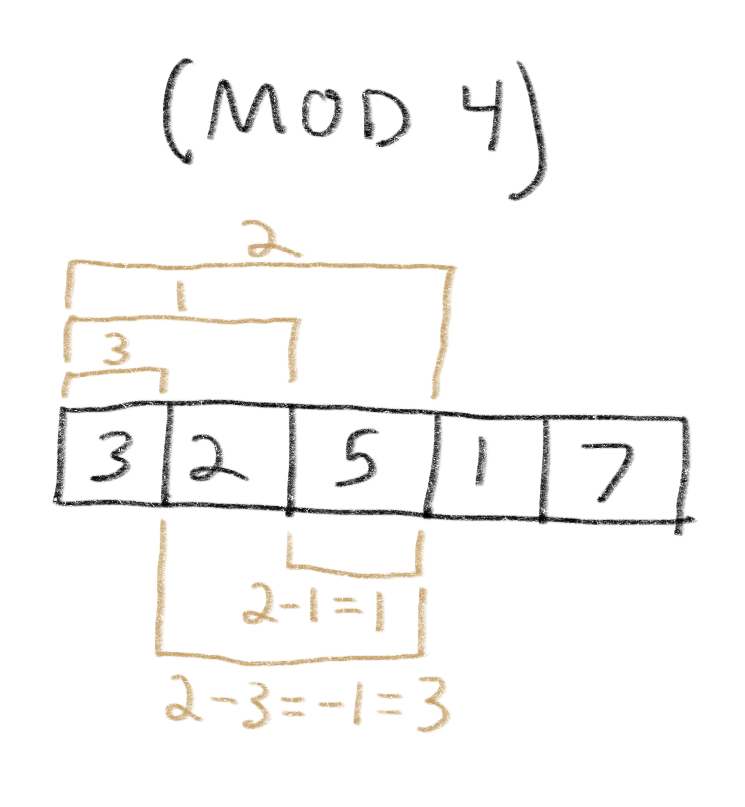
Let’s consider the relations between subarray modulo-sums for [3, 2, 5, 1, 7], for modulo 4:
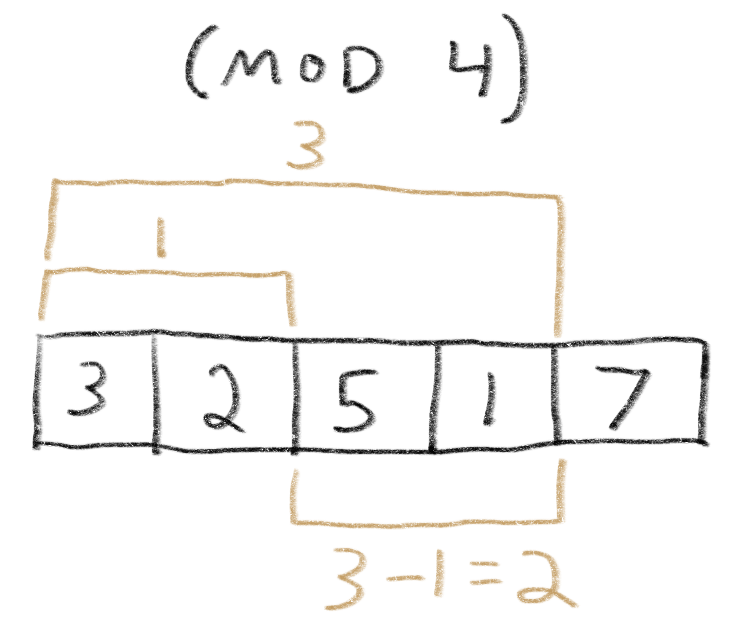
If you subtract the modulo-sum of subarray 0 to 1 from the modulo-sum of subarray 0 to 3, you get the correct modulo-sum for subarray 2 to 3.
Unfortunately, this doesn’t quite work for the subarray of 1 to 2:
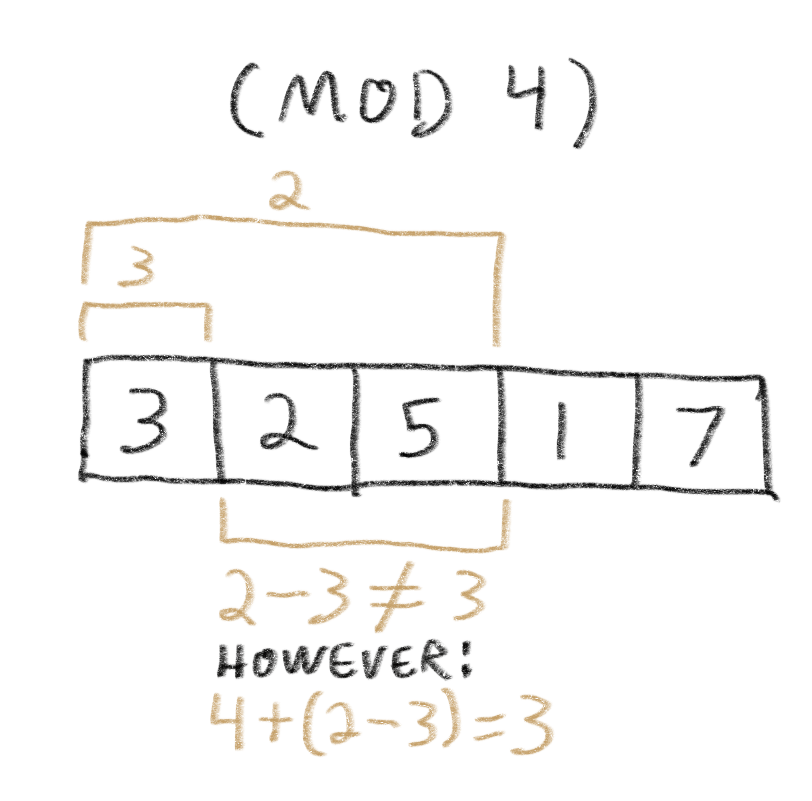
The sum of subarray 0 to 2, minus the sum of subarray 0 to 0, is -1, whereas the sum of subarray 1 to 2 is 3.
However, note that if we add the modulus, 4, to -1, we get the desired answer of 3.
Why does that work?
When dealing with arithmetic constrained by modulo, I like to imagine a wheel with a spinning pointer on it. If we’re using a modulus of 4, for instance, then it’s a wheel divided into 4 sections, labeled 0, 1, 2, 3. Addition moves the pointer one direction; subtraction moves the pointer the other direction.
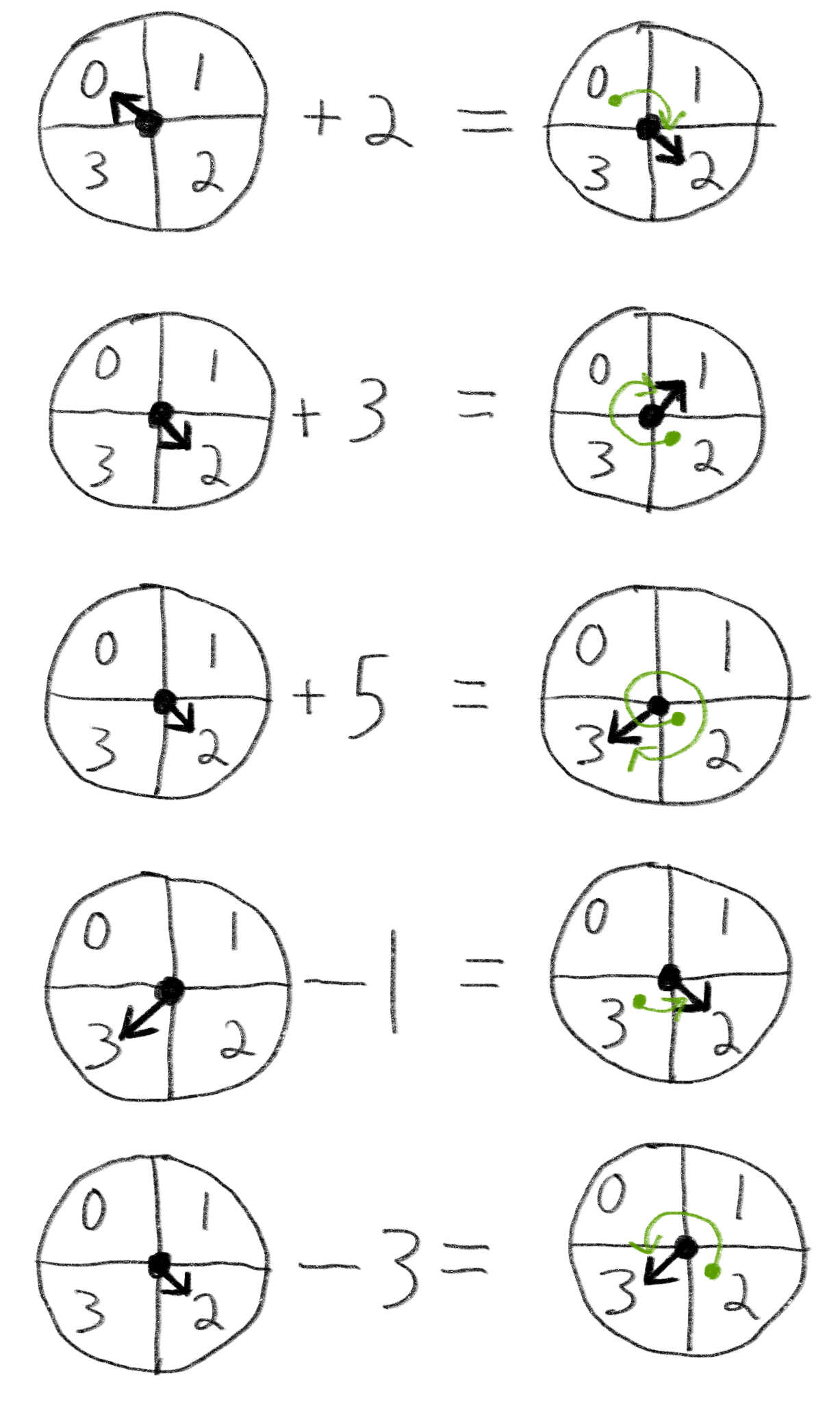
It’s like working on a number wheel instead of working on a number line. As you can see from the last two examples, when we define subtraction in this way, then when the modulus is 4, 3 - 1 = 2 and 2 - 3 = 3, which are the correct answers for the subarray modulo-sums we were considering above.
To find the modulo-sum of any subarray, all we need to do is change the code from the previous section to use this type of subtraction operation. To do that, we perform regular subtraction, but if the difference is negative, add it to the modulus:
class SubarrayModuloSumFinder(val a: Array<Long>, val mod: Long) { val sums = ArrayList<Long>() init { var sum = 0L for (v in a) { sum = (sum + v) % mod sums.add(sum) } } fun sum(i: Int, j: Int): Long { val diff = sums[j] - (if (i > 0) sums[i - 1] else 0L) return if (diff >= 0) diff else mod + diff } } fun main() { val test = SubarrayModuloSumFinder(arrayOf(3L, 2L, 5L, 1L, 7L), 4) println(test.sum(0, 1)) // prints 1 println(test.sum(0, 3)) // prints 3 println(test.sum(2, 3)) // prints 2 println(test.sum(0, 0)) // prints 3 println(test.sum(0, 2)) // prints 2 println(test.sum(1, 2)) // prints 3 println(test.sum(0, 4)) // prints 2 }
We know from the previous section that in O(N) time, we can prepare ourselves to find in O(1) time the modulo-sum of any subarray we’re subsequently asked about.
That algorithm precalculates the modulo-sums for all the subarrays that start at index 0 and end at any other index. We could easily change the code to keep track of which of those subarrays has the highest modulo-sum.
But what if there’s some index i != 0, where the subarray i to j has a higher modulo-sum than the subarray 0 to j has? Let’s think about what would make that possible. Since there are no negative numbers in the array, it can only happen because we’re applying modulo at each step. Otherwise, the sum of subarray 0 to j would always be larger than that of subarray i to j (assuming i < j), since the former is the sum of all the numbers in the latter plus some.
Think about the metaphor of the wheel with a spinning pointer again. If the modulo-sum of subarray 0 to j is smaller than that of subarray i to j, that means the sum of all the numbers in subarray 0 to j was enough to spin the pointer at least one full time around (back to, or past, 0). If we were to remove values from the beginning of the subarray one at a time, moving the spinning pointer in reverse the corresponding amount, when we got to index i the spinner would go back past zero and land on a higher number than the modulo-sum that we started with.
Of course, that doesn’t guarantee this is the largest subarray that ends at index j. If we kept on removing values, it’s possible we’d eventually spin back past 0 yet again and land on an even higher number.
How many values should we remove in order to land on the highest number? The highest possible modulo-sum is the modulus minus 1, since beyond that you go back to 0. To land on modulus minus 1, we’d need to subtract values whose total modulus-sum is equal to our original modulus-sum (of subarray 0 to j) plus 1. What if we can’t do that? Well, the next-best thing would be to land on modulus minus 2, which would require subtracting our original modulus-sum plus 2; and so forth. What we really want is to find the smallest value we can subtract that’s still larger than the modulo-sum of the full subarray 0 to j.
The “values we can subtract” are the modulo-sums of all the subarrays of 0 to i where i < j. As shown here, if we’re trying to find the best subarray ending at index 2, then we’d consider:
In the algorithm given in the preceding section, when we’re looking at index j, we know the modulo-sums of all subarrays with a start index of 0 and an end index <= j. All we need is a way to find the one with the smallest modulo-sum that’s still larger than the modulo-sum of subarray 0 to j. And we need a way that’s faster than O(N), since we’re already inside a loop running N times, and don’t want our total time complexity to jump to O(N2)
The HackerRank page gives an important hint by listing “Binary Search” in the resources section. If we store all the modulo-sums we’ve found so far in a binary tree, then we can use binary search to find one according to our criteria in O(log(N)) time. Most major programming languages have built-in or readily available data structures that can build and search the binary tree (or other structure with the right performance characteristics) so that it’s not necessary to implement it ourselves.
Here’s the full solution (it doesn’t need the code from the previous two sections, that was just for explanatory purposes), excluding the main method you can get from the HackerRank template:
fun maximumSum(a: Array<Long>, m: Long): Long { var max = 0L var sum = 0L var sums = TreeSet<Long>() for (v in a) { sum = (sum + v) % m val closestLargerSum = sums.ceiling(sum + 1) ?: 0 if (closestLargerSum > 0) { max = maxOf(max, m + sum - closestLargerSum) } sums.add(sum) max = maxOf(max, sum) } return max }
Here’s a walkthrough of each step of the loop in this algorithm, for the array [3, 2, 5, 1, 7] with modulus 7 instead of 4:
| j | a[j] | subarray 0 to j | modulo-sum of 0 to j | sorted set of modulo-sums of subarrays 0 to i where i < j | best modulo-sum for any subarray i to j | best modulo-sum so far |
|---|---|---|---|---|---|---|
| 0 | 3 | 3 |
3 | 3 | 3 | |
| 1 | 2 | 3,2 |
5 | 3 |
5 | 5 |
| 2 | 5 | 3,2,5 |
3 | 3,5 |
5 (subtracting 5 from 3) | 5 |
| 3 | 1 | 3,2,5,1 |
4 | 3,5 |
6 (subtracting 5 from 4) | 6 |
| 4 | 7 | 3,2,5,1,7 |
4 | 3,4,5 |
6 (subtracting 5 from 4) | 6 |